Skip to contents

spagg

spagg.Rmd

Introduction

In this vignette, we illustrate how to use the spagg package to analyze multiple spatial point patterns. In particular, we will show how to use the functions in this package to construct an aggregate spatial summary statistic across point patterns grouped together by some higher level factor, such as by tissue sample. We will then use this aggregated spatial summary statistic as a predictor in a linear model for a group-level/sample-level outcome.

The motivation behind spagg is that analyses of data from multiplexed immunofluorescence and spatial proteomics platforms may involve multiple regions-of-interest (ROIs) imaged from the same tissue sample. Each ROI shows the spatial location of cells in tissue which can be treated as a spatial point pattern. Access to multiple ROIs per tissue sample can complicate associative analyses seeking to characterize associations between the spatial distribution of cells in tissue and sample-level outcomes because we need to test for an association between a single sample-level outcome (e.g. survival or case/control status) and multiple spatial summary statistics.

This vignette will use simulated spatial point pattern data. To see how this data was generated, please see spagg > data-raw > simdata.R.

Loading in the Data and Plotting

We start by loading in the spagg package and our simulated data. We show the first few lines of the dataset below. The dataset is organized so as to mimic the structure of single-cell, spatial images produced by multiplexed immunofluorescence and spatial proteomics platforms. Each row corresponds to a detected cell, which is enumerated by the cell.id column. The cells are grouped together by samples, denoted by the PID column and by images within those samples, denoted by the id column. The x and y columns give the (x,y) coordinates of each cell. The type column denotes the cell type for the corresponding row. In this simulated dataset, the possible cell types are a and b. Finally, the out column gives the sample-level endpoint with which we are interested in performing associative analyses. In this simulated dataset, the out column is a binary 1 or 0 indicator.

# Load in packages
library(spagg)
library(ggplot2)
library(cowplot)
library(spatstat)
#> Loading required package: spatstat.data
#> Loading required package: spatstat.univar
#> spatstat.univar 3.0-0
#> Loading required package: spatstat.geom
#> spatstat.geom 3.3-2
#> Loading required package: spatstat.random
#> spatstat.random 3.3-1
#> Loading required package: spatstat.explore
#> Loading required package: nlme
#> spatstat.explore 3.3-1
#> Loading required package: spatstat.model
#> Loading required package: rpart
#> spatstat.model 3.3-1
#> Loading required package: spatstat.linnet
#> spatstat.linnet 3.2-1
#> 
#> spatstat 3.1-1 
#> For an introduction to spatstat, type 'beginner'
library(dplyr)
#> 
#> Attaching package: 'dplyr'
#> The following object is masked from 'package:nlme':
#> 
#>     collapse
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union

# Load in data and show first few lines
data(simdata)
head(simdata)
#>   PID            id        x        y cell.id type out
#> 1   1 PID.1.image.1 27.09050 63.03496       1    a   1
#> 2   1 PID.1.image.1 21.97141 63.93355       2    a   1
#> 3   1 PID.1.image.1 18.70571 63.51489       3    b   1
#> 4   1 PID.1.image.1 20.29608 68.71936       4    b   1
#> 5   1 PID.1.image.1 22.74318 69.08458       5    b   1
#> 6   1 PID.1.image.1 17.47202 75.63201       6    b   1

We can plot the images for PID=1. This can be a helpful tool to visually assess variation in the spatial distribution of cells across ROIs.

# Plot the images for PID=1 --

# Save the image IDs
PID.1.image.ids <- unique(simdata$id[simdata$PID == 1])

# Create a list of plots
plot.list <- lapply(1:length(PID.1.image.ids), function(i) list())

# Iterate through the image IDs and create a plot for each
for (id.i in PID.1.image.ids) {
  
  pp <- simdata %>%
          dplyr::filter(id == id.i) %>%
          ggplot(aes(x = x, y = y, color = type)) +
          geom_point() + 
          theme_bw() +
          ggtitle(id.i)
  plot.list[[which(PID.1.image.ids == id.i)]] <- pp
  
}

# Construct the full plot
cowplot::plot_grid(plot.list[[1]], plot.list[[2]], 
                   plot.list[[3]], plot.list[[4]],
                   plot.list[[5]], nrow = 3, ncol = 2)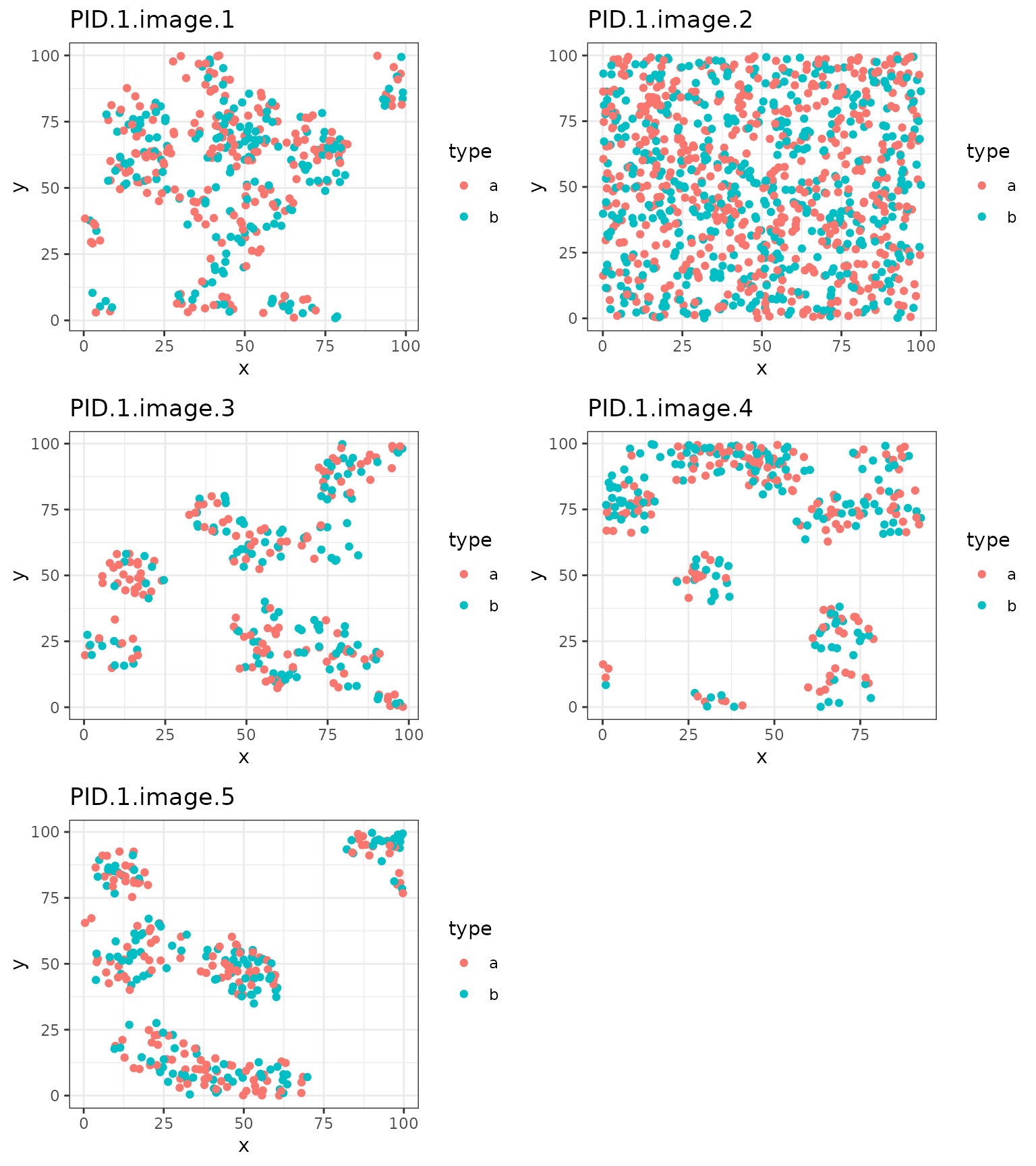

The above plots show simulated data, but illustrate a common challenge that arises in analyzing grouped point patterns reflecting multiple ROIs of a tissue sample: heterogeneity in the spatial clustering patterns. Each ROI shows a different clusterig pattern among the a and b cell types.

We are going to use the spatial summary statistic, Ripley’s K, to characterize the degree of adherence to clustering, repulsion, or complete spatial randomness in each ROI. The spagg package the contains five approaches for handling multiple spatial summary statistics for associative analyses. Three of these approaches are weighted aggregations of the spatial summaries using fixed weights. The other two are ensemble approaches which generate random weights used to construct weighted aggregations. Within each ensemble replication, we test for an association between the weighted aggregation and the sample-level outcome. We then ensemble the resulting p-values for an omnibus test.

We first start by illustrating the weighted aggregations.

Weighted Aggregations

We will first consider different approaches to averaging Ripely’s K across ROIs within a sample. Let’s start by defining some notation. Suppose for sample ii we have RiR_i ROIs. Let nirn_{ir} be the number of cells in sample ii ROI rr. Let AirA_{ir} represent the area of sample ii ROI rr. Let K̂ir\hat K_{ir} represent the spatial distribution of cells evaluate at radius rr.

spagg contains implementations for the following three weighted averages:

  1. K‾iDiggle=1∑r=1Rinir∑r=1RinirK̂ir\begin{equation*} \bar K_i^{Diggle} = \frac{1}{\sum_{r=1}^{R_i} n_{ir}} \sum_{r=1}^{R_i} n_{ir} \hat K_{ir} \end{equation*}

  2. K‾iBaddeley=1∑r=1Rinir2∑r=1Rinir2K̂ir\begin{equation*} \bar K_i^{Baddeley} = \frac{1}{\sum_{r=1}^{R_i} n^2_{ir}} \sum_{r=1}^{R_i} n^2_{ir} \hat K_{ir} \end{equation*}

  3. K‾iLandau=∑r=1RiAir∑r=1Rinir∑r=1Rinir2AirK̂ir\begin{equation*} \bar K_i^{Landau} = \frac{\sum_{r=1}^{R_i} A_{ir}}{\sum_{r=1}^{R_i} n_{ir}} \sum_{r=1}^{R_i} \frac{n^2_{ir}}{A_{ir}} \hat K_{ir} \end{equation*}

K‾iDiggle\bar K_i^{Diggle} (Diggle, Lange, and Beneš (1991)), K‾iBaddeley\bar K_i^{Baddeley} (Baddeley et al. (1993)), and K‾iLandau\bar K_i^{Landau} (Landau, Rabe-Hesketh, and Everall (2004)) were each proposed as approaches to aggregating replicated Ripley’s K statistics. The motivation behind each of these aggregations is to weight each Ripley’s K statistic by its sampling variance. However, the sampling variance is generally difficult to write down explicitly for Ripley’s K so each method relies on an approximation. The accuracy of the approximation relies on whether the intensity of the spatial point pattern (the ratio of the number of cells divided by the image area) is consistent or varied across ROIs. If the intensity is consistent, all methods should yield similar average Ripley’s K statistics and, in turn, perform similarly-well for hypothesis testing. If the intensity is different across ROIs, and also informative in predicting the outcome, the Landau mean may perform better.

We first consider a univariate analysis where we analyze only one cell type. We start with cell type a only and its associations with sample-level outcomes. We estimate Ripley’s K for r=30r=30 on each ROI. Note this may take several seconds (up to 30 seconds) to run.

# Set the radius
r <- 30

# Save the image IDs
ids <- unique(simdata$id)

# Initialize a data.frame to store the results for each ROI
cell.a.results <- simdata %>% 
  dplyr::select(PID, id) %>%
  dplyr::distinct() %>%
  dplyr::mutate(spatial = NA,
                npoints = NA,
                area = NA)
 
# Iterate through the ROIs (this will take a few seconds)
for (i in 1:length(ids)) {
  
 # Save the ith image
 image.i <- simdata %>%
   dplyr::filter(id == ids[i]) %>%
   dplyr::select(x, y, type)

   # Convert to a point process object
   w <- spatstat.geom::convexhull.xy(image.i$x, image.i$y)
   image.i.subset <- image.i %>% dplyr::filter(type == "a")
   image.ppp <- spatstat.geom::as.ppp(image.i.subset, W = w)
   spatstat.geom::marks(image.ppp) <- image.i.subset$type

   # Compute Kest
   Ki <- spatstat.explore::Kest(image.ppp, r = 0:r)
  
   # Calculate the number of points
   npoints.i <- spatstat.geom::npoints(image.ppp)
   
   # Calculate the area
   area.i <- spatstat.geom::area(image.ppp)
  
   # Save the results
   cell.a.results[cell.a.results$id == ids[i],]$spatial <- Ki$iso[r+1]
   cell.a.results[cell.a.results$id == ids[i],]$npoints <- npoints.i
   cell.a.results[cell.a.results$id == ids[i],]$area <- area.i
}

# View the first few rows
head(cell.a.results)
#>   PID            id  spatial npoints     area
#> 1   1 PID.1.image.1 3402.412     206 8298.469
#> 2   1 PID.1.image.2 2779.338     538 9844.653
#> 3   1 PID.1.image.3 2623.948     134 7157.505
#> 4   1 PID.1.image.4 3382.632     151 8314.183
#> 5   1 PID.1.image.5 2911.225     157 7682.093
#> 6   2 PID.2.image.1 2374.916      62 7080.358

We can now visualize the distribution of the spatial summaries within each image as an illustration of the variation in spatial distribution of cells of type a across ROIs.

# Visualize the distribution of spatial summaries within each sample
cell.a.results %>%
  dplyr::mutate(PID = factor(PID)) %>%
  ggplot(aes(x = PID, y = spatial, group = PID)) + 
  geom_boxplot() +
  theme_bw() +
  ggtitle("Ripley's K statistics for ROIs within a each sample") +
  ylab("Kest")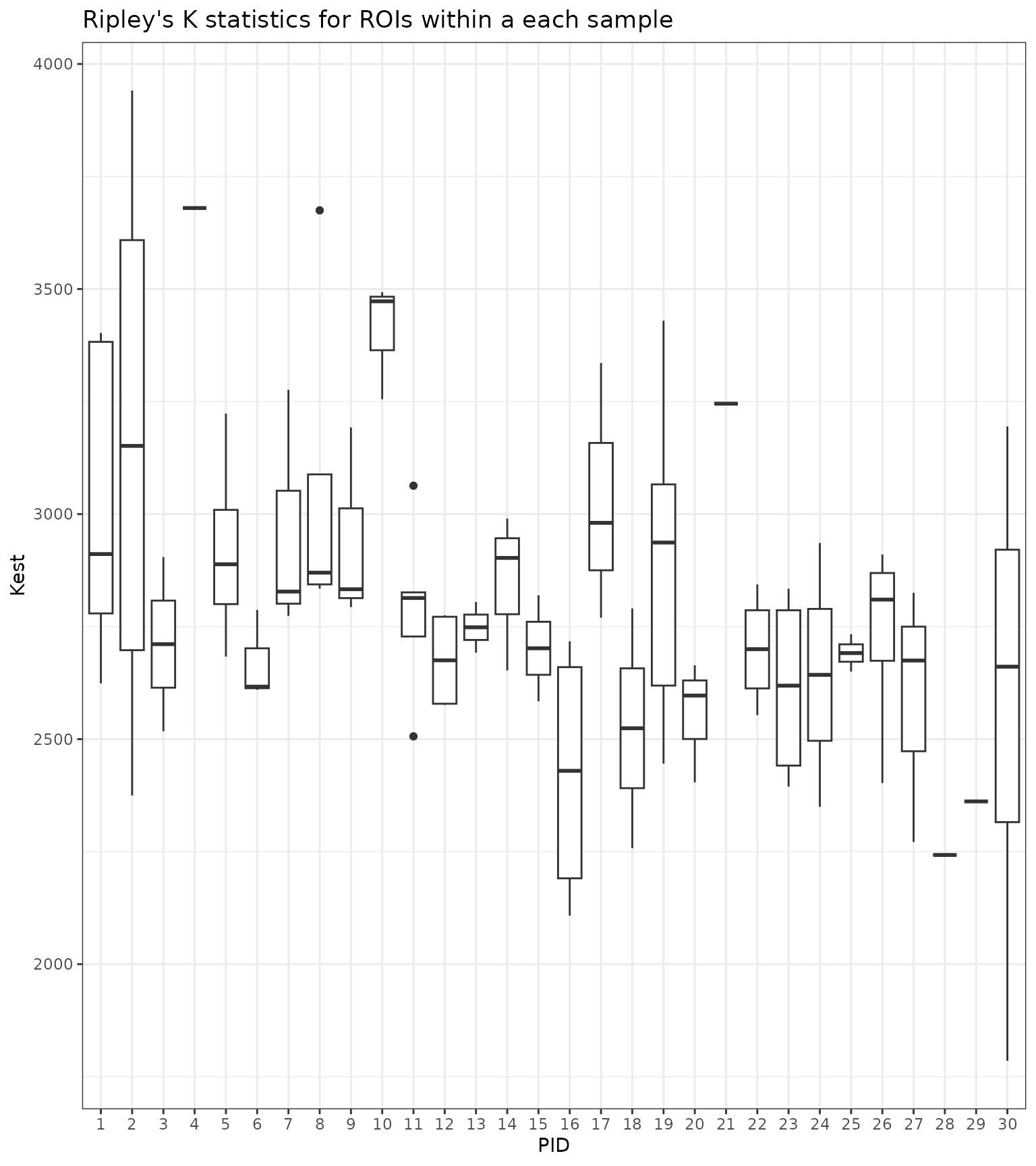

As the above plot illustrates, there can be considerable variation in the spatial summary statistic values within a single sample.

After that, we will compute the weighted averages given above. We will also compute a standard arithmetic mean as a comparison. Below, we visualize the spread of the various spatial aggregation methods within each sample. For some samples, the averages yield similar values. For others, the averages exhibit large variation, suggesting they up- or down-weight certain ROIs depending on the area of the ROI or the number of cells.

# Compute averages
cell.a.results_mean <- cell.a.results %>%
    dplyr::group_by(PID) %>%
    dplyr::summarise_at(dplyr::vars(spatial),
                        list(~mean(.x), 
                             ~landau.avg(K.vec = .x, area.vec = area, n.vec = npoints),
                             ~diggle.avg(K.vec = .x, n.vec = npoints),
                             ~baddeley.avg(K.vec = .x, n.vec = npoints)))

# Plot the averages
cell.a.results_mean %>%
  tidyr::pivot_longer(2:5, names_to = "mean", values_to = "value") %>%
  dplyr::mutate(mean = recode(mean, 
                              "mean" = "Arithmetic Mean",
                              "landau.avg" = "Landau Mean",
                              "diggle.avg" = "Diggle Mean",
                              "baddeley.avg" = "Baddeley Mean")) %>%
  dplyr::mutate(PID = factor(PID)) %>%
  ggplot(aes(x = PID, y = value, group = mean, color = mean)) +
  geom_point() +
  theme_bw() +
  ylab("Average Kest") +
  ggtitle("Averaged Ripley's K within each sample") +
  scale_color_discrete(name = "Aggregation Method")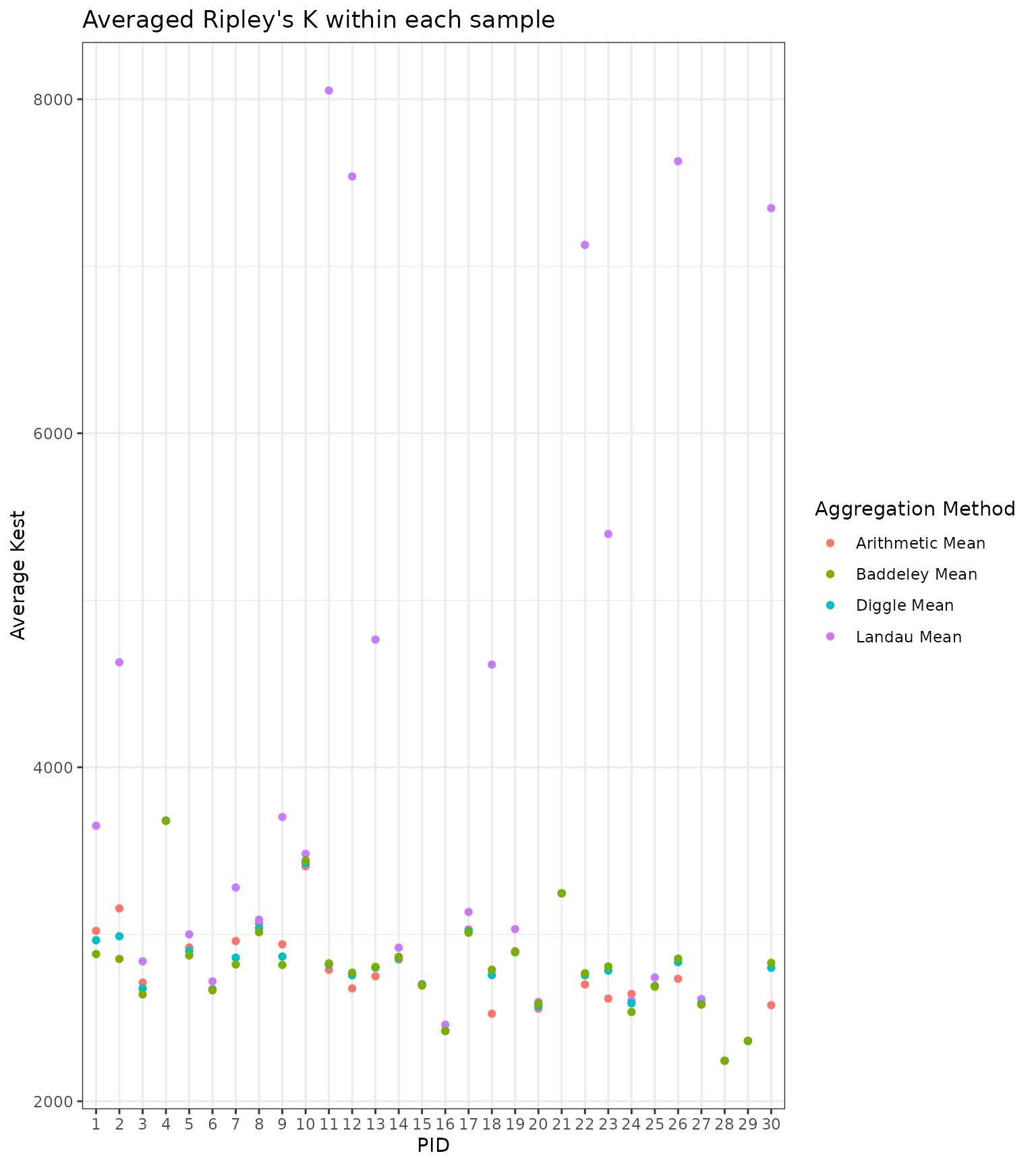

We now have a data.frame with a column corresponding to each average. We can add in the outcome variable, out, so we can do association testing with the aggregated Ripley’s K statistics. We would like to compare if the aggregated Ripley’s K statistics are equal between cases (out=1) and controls (out=0). In other words, we would like to test if the average spatial distribution of cells across ROIs is the same between these two groups.

# First, check the ordering matches
all(unique(simdata$PID) == cell.a.results_mean$PID) # TRUE!
#> [1] TRUE

# Add in the outcome
cell.a.results_mean$out <- simdata %>% 
  dplyr::select(PID, out) %>%
  dplyr::distinct() %>%
  dplyr::select(out) %>%
  unlist()

# Test for an association between CD4 T cell spatial distributions and MHCII-high status
mean.glm <- glm(out ~ mean, data = cell.a.results_mean, family = binomial())
diggle.glm <- glm(out ~ diggle.avg, data = cell.a.results_mean, family = binomial())
baddeley.glm <- glm(out ~ baddeley.avg, data = cell.a.results_mean, family = binomial())
landau.glm <- glm(out ~ landau.avg, data = cell.a.results_mean, family = binomial())

# Save the p-values in a table and display
cell.a.pvals <- data.frame(
  Method = c("Mean", "Diggle", "Baddeley", "Landau"),
  P.Value = c(summary(mean.glm)$coef[2,4], summary(diggle.glm)$coef[2,4], 
              summary(baddeley.glm)$coef[2,4], summary(landau.glm)$coef[2,4])
)

# Show the results
cell.a.pvals
#>     Method     P.Value
#> 1     Mean 0.006060067
#> 2   Diggle 0.023752779
#> 3 Baddeley 0.040878265
#> 4   Landau 0.205325277

Using a standard mean, the Diggle method, and the Baddeley approach, we found a significant association between the spatial distribution of cell type a and outcomes. We did not find this association, however, using the Landau mean.

To explore the varied performance of these methods a bit more, we can plot the intensity of cell type a within each ROI and examine the variation across samples, as shown below. There is considerable variation across samples and considerable variation within some samples. Samples 4 and 6, for example, show very little variation across ROIs. However, Sample 4 only had 1 image. Other samples, showed more variation, like Samples 1 and 2. The overall spread in variation, however, was only between 0.002 and 0.05.

# Calculate intensity for each ROI and plot
cell.a.results %>%
  dplyr::mutate(intensity = npoints/area) %>%
  dplyr::mutate(PID = factor(PID)) %>%
  ggplot(aes(x = PID, y = intensity, group = PID)) + 
  geom_boxplot() +
  theme_bw() +
  ggtitle("Variation in Point Pattern Intensity Within Each Sample")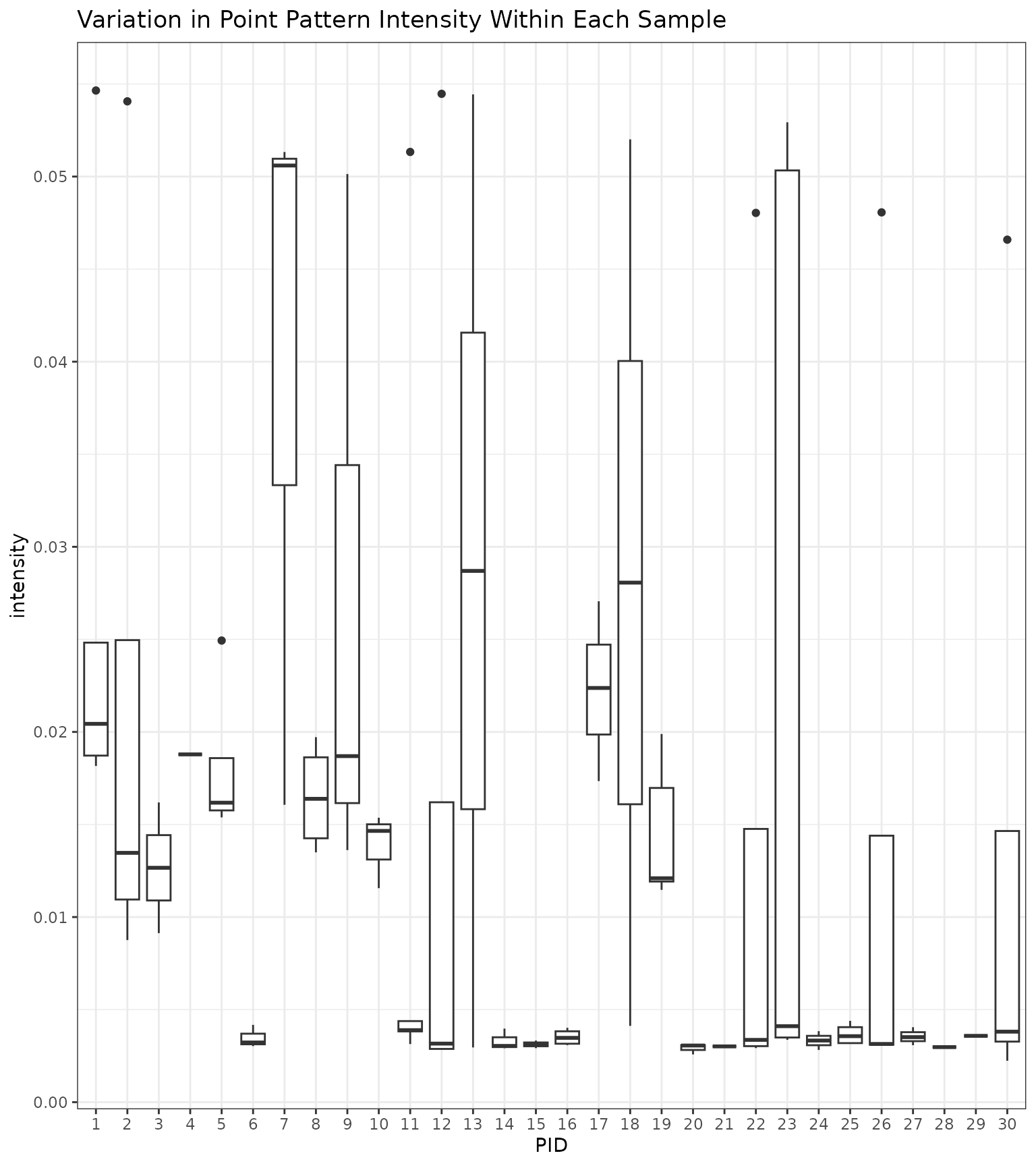


# How many ROIs did each sample have?
simdata %>% dplyr::select(PID, id) %>% dplyr::group_by(PID) %>% dplyr::summarise(n = n()) %>% head(10)
#> # A tibble: 10 × 2
#>      PID     n
#>    <int> <int>
#>  1     1  2272
#>  2     2  1570
#>  3     3   466
#>  4     4   318
#>  5     5  1098
#>  6     6   170
#>  7     7  2292
#>  8     8  1004
#>  9     9  1419
#> 10    10   702

# Calculate the range in intensity
cell.a.results %>%
  dplyr::mutate(intensity = npoints/area) %>%
  dplyr::summarise(min.intensity = min(intensity),
                   max.intensity = max(intensity))
#>   min.intensity max.intensity
#> 1   0.002237422    0.05464895

We can also examine if the intensity differed between outcomes. Below we plot the intensities across ROIs and examine if this associates with case (out=1) or control (out=0) status. Below, we see that there was some variation in ROI intensity across outcomes. Nonetheless, the Landau mean still did not perform best.

# Add in the outcome
cell.a.results$out <- simdata %>%
  dplyr::select(PID, id, out) %>%
  dplyr::distinct() %>%
  dplyr::select(out) %>%
  unlist()

# Plot
cell.a.results %>%
  dplyr::mutate(intensity = npoints/area) %>%
  dplyr::mutate(out = factor(out)) %>%
  ggplot(aes(x = out, y = intensity)) + 
  geom_boxplot() +
  theme_bw() +
  ggtitle("Variation in Point Pattern Intensity Across Outcomes")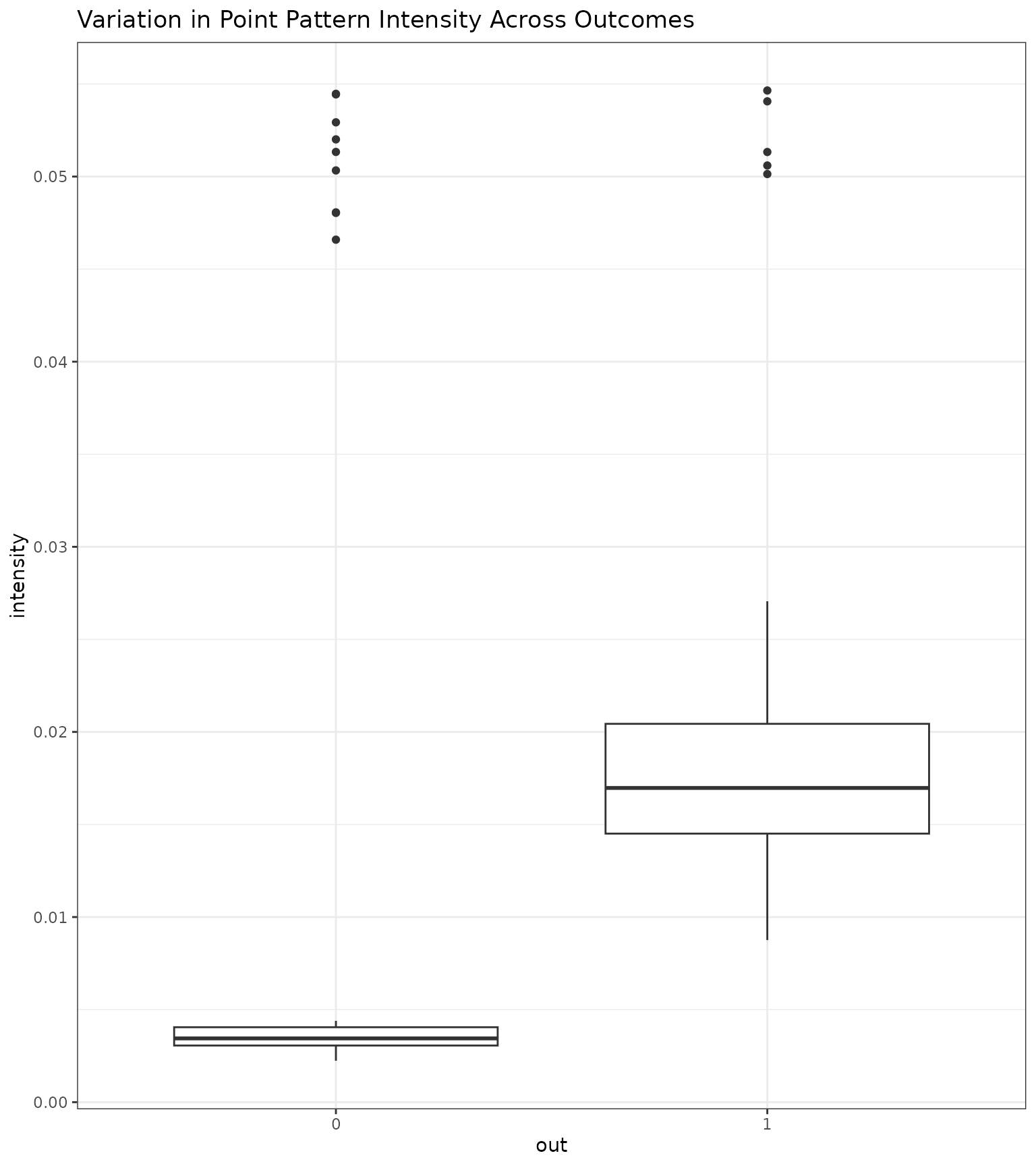

We also consider a bivariate analysis where we examine the bivariate colocalization of cell types a and b. We follow a similar series of steps, but instead use the Kcross function to characterize the colocalization of these cell types.

# Set the radius
r <- 30

# Initialize a data.frame to store the results for each ROI
cell.ab.results <- simdata %>% 
  dplyr::select(PID, id) %>%
  dplyr::distinct() %>%
  dplyr::mutate(spatial = NA,
                npoints = NA,
                area = NA)
 
# Iterate through the ROIs (this will take a few seconds)
for (i in 1:length(ids)) {
  
 # Save the ith image
 image.i <- simdata %>%
   dplyr::filter(id == ids[i]) %>%
   dplyr::select(x, y, type)

   # Convert to a point process object
   w <- spatstat.geom::convexhull.xy(image.i$x, image.i$y)
   image.ppp <- spatstat.geom::as.ppp(image.i, W = w)
   spatstat.geom::marks(image.ppp) <- factor(image.i$type)

   # Compute Kest
   Ki <- spatstat.explore::Kcross(image.ppp, i = "a", j = "b", r = 0:r)
  
   # Calculate the number of points
   npoints.i <- spatstat.geom::npoints(image.ppp)
   
   # Calculate the area
   area.i <- spatstat.geom::area(image.ppp)
  
   # Save the results
   cell.ab.results[cell.ab.results$id == ids[i],]$spatial <- Ki$iso[r+1]
   cell.ab.results[cell.ab.results$id == ids[i],]$npoints <- npoints.i
   cell.ab.results[cell.ab.results$id == ids[i],]$area <- area.i
}

# View the first few rows
head(cell.ab.results)
#>   PID            id  spatial npoints     area
#> 1   1 PID.1.image.1 3352.665     388 8298.469
#> 2   1 PID.1.image.2 2778.717    1010 9844.653
#> 3   1 PID.1.image.3 2695.169     257 7157.505
#> 4   1 PID.1.image.4 3406.225     316 8314.183
#> 5   1 PID.1.image.5 2947.781     301 7682.093
#> 6   2 PID.2.image.1 2449.192     124 7080.358

Following the same steps as above, we will compute the averages within each PID and test for an association with the outcome.

# Compute averages
cell.ab.results_mean <- cell.ab.results %>%
    dplyr::group_by(PID) %>%
    dplyr::summarise_at(dplyr::vars(spatial),
                        list(~mean(.x), 
                             ~landau.avg(K.vec = .x, area.vec = area, n.vec = npoints),
                             ~diggle.avg(K.vec = .x, n.vec = npoints),
                             ~baddeley.avg(K.vec = .x, n.vec = npoints)))

# First, check the ordering matches
all(unique(simdata$PID) == cell.ab.results_mean$PID) # TRUE!
#> [1] TRUE

# Add in the outcome
cell.ab.results_mean$out <- simdata %>% 
  dplyr::select(PID, out) %>%
  dplyr::distinct() %>%
  dplyr::select(out) %>%
  unlist()

# Test for an association between CD4 T cell spatial distributions and MHCII-high status
mean.ab.glm <- glm(out ~ mean, data = cell.ab.results_mean, family = binomial())
diggle.ab.glm <- glm(out ~ diggle.avg, data = cell.ab.results_mean, family = binomial())
baddeley.ab.glm <- glm(out ~ baddeley.avg, data = cell.ab.results_mean, family = binomial())
landau.ab.glm <- glm(out ~ landau.avg, data = cell.ab.results_mean, family = binomial())

# Save the p-values in a table and display
cell.ab.pvals <- data.frame(
  Method = c("Mean", "Diggle", "Baddeley", "Landau"),
  P.Value = c(summary(mean.ab.glm)$coef[2,4], summary(diggle.ab.glm)$coef[2,4], 
              summary(baddeley.ab.glm)$coef[2,4], summary(baddeley.ab.glm)$coef[2,4])
)

# Show the results
cell.ab.pvals
#>     Method    P.Value
#> 1     Mean 0.02393126
#> 2   Diggle 0.01362797
#> 3 Baddeley 0.05261129
#> 4   Landau 0.05261129

Here we found a significant association between the spatial colocalization of cell types a and b with outcomes using a standard arithmetic mean and using the Diggle mean but not using the Baddeley or Landau mean.

Ensemble Approaches

We now illustrate using ensemble testing to test the same hypothesis, whether the spatial distribution of cells is equal between cases (out=1) and controls (out=0). These ensemble approaches consider multiple random weights used to construct the aggregations of the spatial summary statistics. For each set of random weights, we test for an association between the weighted aggregation and outcome. We repeat this for many random weights and combine the resulting p-values using a p-value combination method. For this purpose, we use the Cauchy combination test (Liu and Xie (2020)).

The motivation behind these ensemble approaches is that the best set of weights (the weights that will yield the highest power) is generally unknown at the outset. For this reason, considering many different possible weights may gain us more power because we may capture the true relationship between the aggregated spatial summary statistics and sample-level outcome through randomly simulating weights.

spagg contains implementations for two different approaches:

  1. : in this approach, spagg randomly generates weights from a standard normal distribution which are used to construct a weighted mean of the Ripley’s K estimates obtained from each ROI. This process is repeated many times. For each random set of weights, the association between the weighted mean spatial summary and sample-level outcomes is tested. The resulting p-values are combined using the Cauchy combination test. This approach is contained in the ensemble.avg function.

  2. : in this approach, spagg randomly generates weights from a standard normal distribution and uses these weights as well as the number of cells in each ROI to construct a weighted mean of Ripley’s K estimates. This process is repeated many times and the resulting p-values are combined using the Cauchy combination test. This approach is contained in the combo.weight.avg function.

We now run these approaches to testing for the univariate analysis using the cell.a.results data.frame we constructed above which contains the Ripley’s K value at r=30.

# Run each ensemble test
ensemble.res <- ensemble.avg(data = cell.a.results, 
                             group = "PID", 
                             outcome = "out", 
                             model = "logistic")

combo.res <- combo.weight.avg(data = cell.a.results, 
                              group = "PID", 
                              outcome = "out", 
                              model = "logistic")

# Add the p-values to the results above
cell.a.pvals <- rbind.data.frame(
  cell.a.pvals,
  data.frame(
    Method = c("Ensemble", "Combo"),
    P.Value = c(ensemble.res$pval, combo.res$pval)
  )
)

# Print the results
cell.a.pvals
#>     Method     P.Value
#> 1     Mean 0.006060067
#> 2   Diggle 0.023752779
#> 3 Baddeley 0.040878265
#> 4   Landau 0.205325277
#> 5 Ensemble 0.009344770
#> 6    Combo 0.020319545

Here, the mean and the ensemble approaches yielded the lowest p-values. The combo approach also yielded a low p-value. This suggests some concordance among the methods in detecting a significant association between the spatial distribution of cell type a and case/control status.

We can also perform ensemble testing for the bivariate case. We show how to do this below using the cell.ab.results object.

# Add the outcome back into the data
cell.ab.results <- left_join(cell.ab.results, 
                     simdata %>% dplyr::select(id, PID, out) %>% distinct(), 
                     by = c("id", "PID"))

# Run each ensemble test
ensemble.res <- ensemble.avg(data = cell.ab.results, group = "PID", 
                             outcome = "out", model = "logistic")

combo.res <- combo.weight.avg(data = cell.ab.results, group = "PID", 
                              outcome = "out", model = "logistic")
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

# Add the p-values to the results above
cell.ab.pvals <- rbind.data.frame(
  cell.ab.pvals,
  data.frame(
    Method = c("Ensemble", "Combo"),
    P.Value = c(ensemble.res$pval, combo.res$pval)
  )
)

# Print the results
cell.ab.pvals
#>     Method    P.Value
#> 1     Mean 0.02393126
#> 2   Diggle 0.01362797
#> 3 Baddeley 0.05261129
#> 4   Landau 0.05261129
#> 5 Ensemble 0.02104012
#> 6    Combo 0.02473175

Here, the ensemble and combo approaches yielded low p-values, suggesting the spatial colocalization of cell types a and b is associated with the outcome.

References

Baddeley, AJ, RA Moyeed, CV Howard, and A Boyde. 1993. “Analysis of a Three-Dimensional Point Pattern with Replication.” Journal of the Royal Statistical Society: Series C (Applied Statistics) 42 (4): 641–68.
Diggle, Peter J, Nicholas Lange, and Francine M Beneš. 1991. “Analysis of Variance for Replicated Spatial Point Patterns in Clinical Neuroanatomy.” Journal of the American Statistical Association 86 (415): 618–25.
Landau, Sabine, Sophia Rabe-Hesketh, and Ian P Everall. 2004. “Nonparametric One-Way Analysis of Variance of Replicated Bivariate Spatial Point Patterns.” Biometrical Journal: Journal of Mathematical Methods in Biosciences 46 (1): 19–34.
Liu, Yaowu, and Jun Xie. 2020. “Cauchy Combination Test: A Powerful Test with Analytic p-Value Calculation Under Arbitrary Dependency Structures.” Journal of the American Statistical Association 115 (529): 393–402.